Willkommen in unserer Bastelstunde!!!! :)
Werkzeug:
Hirnschmalz, Bleistift, Schmierpapier
Für die Weicheier, Bleistiftspitzer, Gurtfahrer, Clickiesbenützer, Durchschlagschutzmontierer etc.. (also ich) auch diverse Mathematikbücher, Formeln, Dreieck blabla...
Worum geht es? Für eine Maschine wurde ein reibschlüssiger Kegelradantrieb benötigt. Die Berührungslinie der Kegelräder wurde gesucht. Die Aufgabe wurde am MTB Downhill Forum www.downhill-board.com gesucht und mit Hilfe eines Mathematikers (Herr Track aus Wien) gefunden. Eines von vielen netten Beispielen wie Mathematik in der Praxis, hier der allgemeine Maschinenbau, benötigt wird.
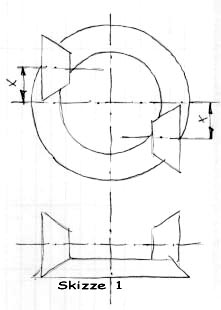Aufgabenstellung: Ein großes Kegelrad treibt reibschlüssig 2 kleine Kegelräder an, die symmetrisch außerhalb der Mitte angeordnet sind (siehe Skizze 1).
Eine Linienberührung ist für die sichere Übertragung des Drehmomentes notwendig.
Gesucht: Die Funktion der Kurve der kleinen Kegelräder, damit das in der CNC-Maschine programmiert werden kann.
Lösung:
Die Lösung soll in drei große Abschnitte unterteilt werden:
- 1.) Aufstellen der Hyperbelgleichung
- 2.) Bestimmung des zugehörigen Radius
- 3.) Dies ist dann die Gleichung der Erzeugenden.
1. Aufstellen der Hyperbelgleichung
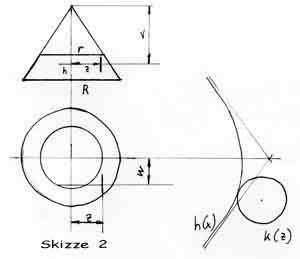
Skizze 2: Gegeben ist: r , R , h , w , v
Wir denken uns einen dünnen Kreis mit Radius k in Abstand z zur x, und Abstand v zur y-Achse
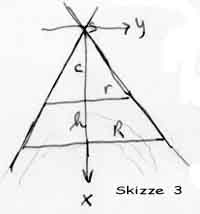
1.1 Gleichung der Asymptoten (Skizze 3)
c/r = (c+h)/R
Gleichung der Asymptoten: y = r / c * x = R / (c+h) * x
1.2 Gleichung der Hyperbel, entlang der Kreis K berührt
Der Abstand z bedingt den Scheitel a durch
y = R / (c+h) * x , y = z , z = R / (c+h) * x , x = z * (c+h) / R
a = z * (c+h) / R
1.3 Gleichung der Hyperbel (Skizze 4)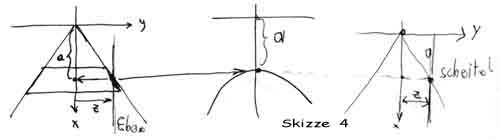
Da die Asymptoten lauten: y = b / a * x und y = R / (c+h) * x
folgt b / a = R / (c+h)
b = a * R / (c+h) = z * (c+h) / R * R / (c+h) = z
folgt b²x² - a²y² = a²b² , wobei a = z * (c+h) / R und b = z ist.
1.4 Ermittlung des Kreises (Skizze 5)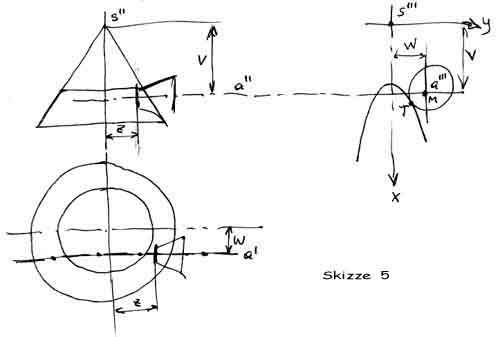
M hat die Koordinaten M (v,w) die gegeben sind, und den Radius k
Die Hyperbel hat die Gleichung b²x² - a²y² = a²b²
Der Kreis hat die Gleichung (x-v)² + (y-w)² = k²
i) b²x² - a²y² = a²b²
ii) (x-v)² + (y-w)² = k²
Das sind 2 Gleichungen für 3 Unbekannte x , y , k
Nochmal zur Erinnerung: Wir suchen die Kurve des kleinen Kegelrades, dazu brauchen wir den Radius des gedachten kleinen Kreises k in der bestimmten Position x , y
Wir benötigen also noch eine dritte Gleichung. Die bekommen wir durch folgende Überlegung:
Im Berührpunkt T (x,y) berühren sich eben die beiden Kurven i) und ii) (no na *gg*), das heißt aber, die Anstiege der Tangenten müssen gleich sein!
Wie bekannt, ist der Anstieg der Tangenten die 1. Ableitung.
i) differenzieren:
2b²x - 2a²y * y´ = 0
b²x - a²yy´ = 0
y´ = b²x / a²y
ii) differenzieren:
2(x-v) + 2(y-w) * y´ = 0
y´= - (x-v) / (y-w)
i) und ii) gleichsetzen:
b²x / a²y = - (x-v) / (y-w)
iii) b²x / a²y + (x-v) / (y-w) = 0
2. Ermittlung des Radius:
Das Lösen dieses Systems i) , ii) und iii) liefert T (x,y) und den Radius k
Alle Ergebnisse enthalten die Variable z
3. Gleichung der Erzeugenden: Dieser Wert k = k (z) ist nun bereits die Gleichung der gesuchten Kurve!